This is part 1 of a series on communicating securely.
The most secure method is to probably just meet in person, preferably in secret, and communicate verbally. While this may not be convenient all the time, this is definitely not practical if the sender and the receiver are not close by.
Long distance communication introduces a new party - the medium of communication. It could be
- another person, who will travel and deliver the message to the recipient personally,
- an organized postal network
- network cables
- a frequency of the electromagnetic spectrum
- and so on.
Regardless of what medium is used, the medium is always compromisable. You can bribe/torture people, tap into the broadcasted frequency and intercept the digital signals passing through the cables.
Secure communication has been a problem for humanity for a really long time now. Naturally, solutions to it have been devised. Some of them more robust and fool-proof than the others.
Before we delve further, it is necessary to look at some terminologies on this subject.
- Plaintext - The text that needs to be protected and delivered to the recipient.
- Ciphertext - The text that is being transferred after processing the plaintext in some way.
- Key - An optional entity that is used in the process of conversion of plaintext to ciphertext.
- Algorithm - The processing logic that converts plaintext to ciphertext.
Data Hiding
One of the first techniques developed can be broadly grouped under Data Hiding. It is when the data that is transmitted is concealed from the interceptor. This is also called Steganography.
Some of the concealment techniques involve writing the data in the body of the messenger, using invisible inks that only reveal the text under certain conditions (lights or chemical reactions), and manually or digitally encoding audio or text signals in a non-suspicious image or video.
In Greece, a ruler named Histiaeus tattooed messages on the shaved head of the messenger. When their hair grew back, the prisoner was sent off to their target.
Data Encryption
The techniques used above are called encoding - to mean that the data can still be decoded without access to any type of ‘secret password’ (or ‘key’).
Encryption relies on converting the plaintext to ciphertext using any well-known algorithm with a secret key. The resultant ciphertext can only be converted back to plaintext using a similar key and the same algorithm. Mathematics is the basis of encryption techniques.
All these techniques do not rely on keeping the algorithm secret. The only condition for these techniques to work is to keep the key secret. While it might intuitively sound less secure to reveal the algorithm, there are a few benefits
- Coming up with a secure algorithm might be difficult.
- Once compromised, changing the key is easy, whereas changing the algorithm is not.
- If the algorithm is public, it will eventually evolve to be the strongest version of itself because everyone would have reviewed it and made improvements to it. (And likewise, reject insecure ones.)
- Widespread adoption is easy. If most people know the algorithm, all you need to do is just agree on a key, and then start sending messages.
An interesting manual encryption technique is the Caesar Cipher. Julius Caesar is credited with first using this. To send a message using this technique, simply shift each letter of the initial text (also called plaintext), by a certain number of alphabets. The receiver had to know the “shift key” to be able to decode the message correctly.

The receiver would need to shift the ciphertext by 3 characters in the opposite direction to get back the plaintext.
The encryption algorithms are broadly divided into two classes based on the type of key that is used in the process.
Symmetric key
When the same key is used for both the encryption and the decryption process, such an algorithm is called a symmetric key encryption algorithm.
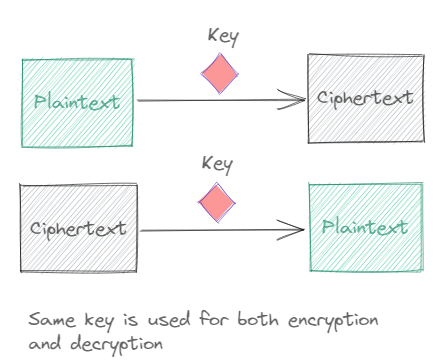
The above example of Caesar Cipher is an example of Symmetric encryption. Modern symmetric key algorithms (for example the AES) are very secure though and unlike the Caesar cipher, cannot be decrypted by a middle school kid without the key.
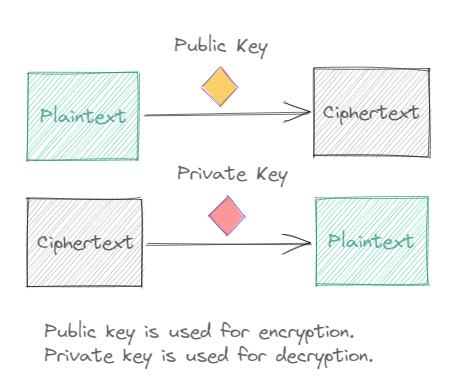
Asymmetric key
As you might have guessed already, here the encryption and decryption process don’t use the same key. Instead, what we have is a keypair. A pair of keys {k1, k2} such that a message encrypted with k1 can be decrypted by k2, while a message encrypted with k2 can be decrypted by k1.
This has some interesting implications.
- First, the sender and receiver do not have the same keys.
- Secondly, access to only one of the keys is necessary to decrypt the message.
So only the key used for decryption needs to be private. The other key can be distributed to everyone and made public. If anyone wishes to communicate with the person, they can encrypt the message using the key that was made public (public key) of the receiver. The receiver can then decrypt this message using the other key of this keypair that they have kept private (private key).
The following is the general protocol to use these algorithms.
- Every person/entity would generate a public-private keypair.
- They would then distribute the public key to everyone who wishes to communicate with them.
- Upon receiving a message, private key will be used for decryption.
For the fact that the sender or receiver need not secretly exchange a common key to encrypt the message in the first place, this class of asymmetric algorithms are also called Public Key encryption algorithms.
Equally interesting is the mathematics behind this. As an example, let us look at a simple watered-down version of the RSA algorithm.
Consider the following algorithm.
m, n, a b and c are positive numbers.
m is the plaintext encoded into a number.
c is the ciphertext.
mod is the modulo operator denoting the remainder of a division. 10 mod 3 = 1 as 9 is a multiple of 3.
- Public Key ->
(n, a) - Private Key ->
(n, b) - Encryption Algorithm ->
c = (m^a) mod n - Decryption Algorithm ->
m = (c^b) mod n
While the algorithm looks simple, not all numbers satisfy the above equations. However, the real beauty of this algorithm lies in the fact that given a sufficiently complex public key, that is given n and a, it is almost impossible to determine the private key b.
Consider the following example. The numbers below are not magic numbers and can be generated based on the theory on this subject.
- Public Key ->
(22, 3) - Private Key ->
(22, 7)
For simplicity, let us assume that the message to transmit is 5.
The encrypted cipher text is therefore 5^3 mod 22 = 15.
15 is transmitted to the receiver.
The receiver calculates plain text as 15^7 mod 22 = 5.
Is this enough?
A combination of asymmetric and symmetric encryption algorithms powers everything today including the modern internet. The algorithms are battle tested and the private keys are indeed kept private by the strongest digital vault mechanisms available.
However… this is still not enough. The next post will cover the new problems in the current day and age and how we can solve them.